The Sphere Packing Problem : Dimension 8
A few days back, I was sitting silently in a lecture room of my Institute waiting for a mathematics seminar to begin. The topic had been stated as -“The Sphere Packing Problem — A Breakthrough”. The speaker was Shobha Madan, Professor of Mathematics at Indian Institute of Technology, Goa. The abstract that had been mailed to us regarding the talk had hinted at the fact that there was something interesting in store for us, but the actual beauty of the breakthrough became apparent only during the seminar as she took us through a fascinating ride in the world of mathematics. I give here an overview of the talk and hence, of the breakthrough that has applications in fields you could never have expected!
So what exactly is this Sphere Packing Problem? It involves finding the most efficient way (maximum occupied region to unoccupied region ratio- area in 2 dimensions, volume in 3 dimensions) to pack identical objects equivalent to the sphere in 3-D, which would be an interval of fixed length in the one dimensional world and a circle in 2-D. When you consider the problem in 1-D, the solution is quite obvious — the intervals of fixed length can sit next to each other without leaving any gap on the 1-D number line. When it comes to 2-D, there are two ways for the circles to occupy the plane: the square packing and the hexagonal packing (Refer to the image).
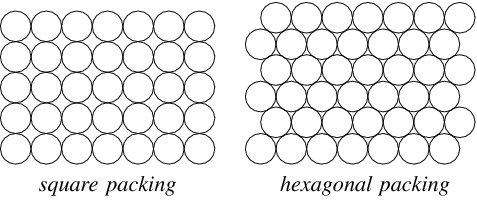
Italian mathematician and astronomer, Joseph Louis Lagrange proved in the 18th century that the highest density arrangement of circles (of equal radii) in the plane would be given by the hexagonal packing arrangement. The density of this packing comes out to be π/12 which is approximately equal to 0.74048. In 3-D, the sphere packing problem was initially termed as the Cannonball problem because of the story that led to the consideration of the problem. Sir Walter Raleigh (who was a poet, politician, spy and several other things!) had asked English mathematician and astronomer Thomas Harriot about which way of stacking cannonballs on the deck of his ships is most efficient. Harriot then approached German astronomer and mathematician Johannes Kepler who conjectured that the face-centered cubic packing and the hexagonal closed packing would be the most efficient arrangements (Refer to image) in a 3-D volume.

The final proof to the Kepler’s Conjecture was completely accepted only recently (in 2017), the journey towards the proof involving the work of generations of mathematicians, the first step being taken by German mathematics prodigy Carl Friedrich Gauss. In fact, in 1900, David Hilbert had included Kepler’s Conjecture as a part of the eighteenth problem of the famous twenty three unsolved problems of mathematics, which largely determined the work done by mathematicians throughout the 19th century.
The breakthrough that the seminar was focused on can be discussed only when we jump into higher dimensions, where visualization becomes impossible! It involves a solution to the sphere packing problem in the 8th dimension and the 24th dimension. Although the mathematics of it can’t be covered in the article, the beauty and consequences of it can definitely be illustrated! Along with other mathematicians, the work involved contribution from Noam Elkies (Professor of mathematics at Harvard University and a chess master!) and Henry Cohn (Senior Principal Researcher at Microsoft Research and adjunct Professor at MIT) who together used linear programming methods to develop the upper bounds for the sphere packing density problem. The graph below shows that the most efficient packing line touches the upper bound line (developed by Cohn and Elkies) in dimension 8 and dimension 24.
The upper bounds developed by Cohn and Elkies were used by Maryna Viazovska (Ukrainian mathematician) in proving that 𝐸8 lattice would be the most dense packing possible in 8 dimensions. She solved the problem in the year 2016. In contrast to the work done for proving the problem in 3-D which required complex computer calculations, her proof was comparatively simple. Interestingly, it is believed that the famous Theory of Everything (which fascinates scientists, mathematicians and philosophers) could be hidden in this beautiful 𝐸8 lattice. The image below is a 2-D projection of this 8 dimensional lattice and the colors and patterns are not random at all! They reflect certain aspects of the actual 8-D lattice.
Later, Maryna worked in collaboration with Cohn, Abhinav Kumar (Indian mathematician and Professor of mathematics at MIT), Stephen Miller (Professor of mathematics at The State University of New Jersey) and Danylo Radchenko (PhD student at Max Planck Institute for Mathematics) to prove that the Leech lattice would be the densest possible packing in 24 dimensions. The Leech lattice has application in error-correcting codes. The study of higher dimensions can benefit us in several unexpected fields, which even includes the field of medicine! The study can also help understand the structure of quasi-crystals. In the graph mentioned before, in addition to dimension 8 and dimension 24, it can be seen that the best packing line has a local maxima in dimension 16 and dimension 32. Is there anything special about dimensions that are a multiple of 8? Well, mathematicians are still working on it and it wouldn’t be a long time before another mathematical brain comes up with another fascinating breakthrough that excites the mathematical community!
